Nurikabe

Generating and Auto-solving

Nurikabe is a logic puzzle I came across in a puzzle magazine I got for Christmas (thanks Mom P!). They're a lot of fun. See here for a description/tutorial, and here for an explanation of this interesting Japanese word.

Since there were only five puzzles in the magazine, I started thinking about how a computer program could generate nurikabe puzzles. It shouldn't be hard to generate nurikabe "mazes" that satisfy the game constraints. However, like most logic puzzles, it seems like the hard part of generating nurikabe is guaranteeing that the ones you produce are solvable. For that, the only way I know is to try to solve them, whether manually or by writing an auto-solver. So below is a draft of some rules for an automatic nurikabe solver to follow. This would be a fun program to write!

According to Brandon McPhail's thesis, nurikabe is NP-complete. What does this imply for writing an auto-solver? That for sufficiently large puzzles, if we wanted to do an exhaustive search for solutions, it would take much longer than we can afford to wait.¹ (Or else we make computer science history by solving an NP-hard problem in polynomial time.) Does this mean that writing a nurikabe solver, and possibly generator, is a lost cause? Theoretically, perhaps, but practically, I don't think so. When I solve a nurikabe puzzle by hand, it doesn't take me exponential time. I don't go six levels deep into hypotheses in order to find out what square to color black or white next. Usually there are deterministic ways to move forward, i.e. you can eliminate possibilities without much searching through potential moves. (Of course, this may be because the puzzles I try to solve are those invented and tested by humans to be not-too-hard for humans.) My hope is that using mostly deterministic methods, an auto-solver can either solve the puzzle in a reasonable amount of time, or give up. A non-exhaustive solver won't be able to prove in every case whether there is exactly one solution to a puzzle, but maybe in most cases, or many cases, it can do a good enough job by doing this reduced task: showing that there is exactly one solution reachable by a fairly thorough application of a set of mostly-deterministic methods typical of what a human is likely to be able to use. I.e. showing that the puzzle is not too hard, which is really in some ways better for what I want (making puzzles for humans) than showing that the puzzle is has exactly one solution.

One question that arises about the generate-and-auto-solve approach is, how efficient will this be? What proportion of well-formed nurikabe puzzles are solvable? Will I have to generate 100,000 puzzles to find one good one? I have no idea what the answer is. If the proportion of good ones is small, would generation heuristics help much? E.g. if the islands are kept fairly narrow, will that help? One could look at a collection of human-designed nurikabe puzzles and try to come up with heuristics.

Maybe an approach from a different direction would yield better results. Instead of (1) generate a random, well-formed nurikabe puzzle and then (2) check how solvable it is, maybe it would be possible to generate a solvable puzzle from the beginning, something like this: start with a blank puzzle, and keep adding clues until it becomes solvable by deterministic methods. I'm not sure of the details of how this would work.

Nurikabe software

There is a free nurikabe-player program for download here (slow connection). It has some predefined puzzles and lets you solve them (assisted by some convenient "smarts"), save progress, and create your own puzzles manually. There is another freeware nurikabe program for Palm here. I haven't played it, but it seems to do the same thing. Neither offers an auto-solver or a puzzle generator. Online nurikabe puzzles can be found here.

Nurikabe constraints

A nurikabe puzzle must conform to these laws:

• A) The black (a.k.a. "water") areas must form one connected region ("wall").
• B) There can never be a 2x2 square of black cells.
• C) Every region ("island") of white ("land") cells must contain exactly one number.
• D) Each number must be in a region of white cells whose cell count is equal to the number.
• E) Diagonal adjacency doesn't count as connectedness.

Corollaries:

• F) Two numbers cannot be connected to each other by white cells. That is, they cannot be in the same region; i.e. the regions they are in cannot touch each other.

Nurikabe-solving rules

OK, now some rules for solving nurikabe:

• 1) Def: A region is "full" if it already has its limit of cells. For a white region, the "limit" is the number written in one of the cells. For a black region, the limit is the number of cells on the board minus the sum of the written numbers.
• 2) Def: A region is "hungry" if it is not full.
• 2a) A white region with no number in it is hungry. (But its limit is unknown.)
• 2.9) [need to renumber] If there are three black cells in an "L" shape, the fourth cell in the square must be white. If there is a square with two black cells and two unsolved cells, check if one of the unsolved cells can be white. If not, the other unsolved cell must be white.
• 3) If there is a full white region [note, this would include any cells with "1" written in them] with adjacent unsolved cells, color those adjacent cells black.
• 3a) I guess you could apply this conversely to a full black region... possibly that could happen before you finish the puzzle by other means! So if there is a full black region, color all the remaining unsolved cells white and you're done.
• 4) If you have two numbers [generalization: two white cells that must belong to distinct regions] adjacent diagonally, the two cells adjacent to both of them must be black. (by F)
• 4a) If you have two numbers [generalization: two white cells that must belong to distinct regions] that are separated by one cell horizontally or vertically, that cell must be black. (by F)
• 4b) Another way of stating 4 and 4a: If you have an unknown cell A such that two or more of its neighbors are white cells that must belong to distinct regions, then cell A must be black. This statement is simpler than separating out 4 and 4a, but separating them may simplify implementation and/or speed processing.
• 5) A hungry region must expand. If there is only one legal cell (of the cells bordering the hungry region) for it to expand into, grow it there. A legal cell is one such that expanding into it will not violate the puzzle constraints. In particular, ...
• 5a) expanding into a given cell is illegal if it cuts off another hungry region (of either color) from any further expansion [elaboration: expanding into a given cell if it cuts off another hungry region (of either color) from the potential for sufficient further expansion]
• 6) If a hungry white [only?] region is surrounded (not immediately) by illegal cells, and the number of legal cells inside the illegal boundary is equal to the number it needs, then expand it into all the legal cells.
• 6a) If a hungry white [only?] region is surrounded (not immediately) by illegal cells, and the number of legal cells inside the illegal boundary is less than the number it needs, flag a contradiction.
• 7) If a hungry white [only?] region has exactly two legal cells into which it could expand, and the legal cells are adjacent diagonally, and there is one unsolved cell that is adjacent to both of them (call it the "threatened" cell), then consider the implications for that threatened cell. If the hungry region only needs one cell, then the threatened cell must be the opposite color. If the threatened cell is adjacent to a white region that must be distinct from the hungry white region, the threatened cell must be black. (by 4a)
• 8) Simple version: if a hungry white region can expand in just two directions, and one direction does not offer sufficient space to complete the region's specified number of cells, the region must expand in the other direction.
• 8a) General version: If a hungry white [only?] region can expand in multiple directions: for each direction D in which it can expand, compute the maximum possible number of cells it can take over (call it M(D)). (Need to elaborate how to compute that!) Call the sum of these maxima S. (S must be >= the limit of the region.) Then for each direction D, if S - M(D) + c < limit (where c is the number of cells already in the region) then expand in direction D. A possible shortcut here (one a human would certainly take) is that if the region can expand in n different directions, and one of them is hard to compute M(D) for, just compute the others. That may tell you that you must expand in direction D. In fact, a different approach to this rule would be to look for areas into which a hungry region could expand, but which offer only a limited possible number of cells -- less than the hungry region needs. Then you know the hungry region must expand in another direction. If there is only one other direction, it must expand that way.
• 10) If there are unsolved cells with no possible path of unsolved cells to reach a hungry white region (where the path is short enough not to overfill the hungry white region), then the unsolved cells must be black.
• 10a) Similarly, if you have an area of unsolved cells, and turning one of them black would cut off other ones from all hungry white regions, then either (i) the ones that would be cut off must all be black, or (ii) the one you were considering turning black must be white. If (i) is impossible, (ii) must be true, and v.v. (This obviously needs further elaboration on how to do it.) For example, suppose there are two unsolved cells, all surrounded by black and border except for one possible "exit" toward a hungry white region. Coloring the one next to the exit black would cut off the other and force it to be black. If this would create a 2x2 black region, then when have a contradition, so the cell next to the exit cannot be black.

These rules are roughly in order of increasing difficulty to apply.

Please let me know of any corrections, improvements, or additions you can think of for the above rules.

Method of applying rules:

(Much of this method is probably applicable to solving many logic games.)

• Need to check for contradictions as we go. We know there is a contradiction, in general, if the constraints (A-F) are violated. In particular, if we have deduced that a particular cell must be white, but we have already marked it as black (or vice versa), then that's a contradiction. Other contradictions could probably be reduced to that case, though that may not be the most efficient way to detect them. E.g. If a hungry region has no legal cells to expand into, that's a contradiction.
• These contradiction checks can form part of the hypothesis-testing mechanism. If we don't have any definite clues about what cell to color black or white, we can try one alternative (especially where we know a particular region must expand into one of two cells) on a trial board, and then proceed; if we hit a contradiction, we know that the hypothesis upon which that trial board branched is false. (But we don't know if it's true unless we go all the way to solving the puzzle. How far do we bother to go?) Then try the other alternative. If one is false, we know the other is true.
• If the original board (not a hypothesis) hits a contradiction, then the original puzzle was not well-formed (i.e. didn't satisfy constraints A-F). (Or else we have a bug, and if so we need to know that!)
• How deep do we want to go into nested hypothesis-checking? Just one level? Up to a configurable number of levels?
• Do we want to go to the trouble of implementing breadth-first rather than just depth-first searches? It would run faster, but take much longer to implement... unless we use an existing code library.
• In general, apply the simpler rules before ones that take longer. (Ideally, you want to be able to save various avenues of exploration on a queue, and evaluate the easiest ones first.)
• A processing loop:
  • 1) Start by placing the whole board on the "invalidated" stack.
  • 2) Have we solved the puzzle yet? (How to check? e.g. see if there is a black region such that cell count = limit) If so, we have *a* solution. If we're working on the original board, this is *the* unique solution, so stop. If we're working on a hypothesis, remember the hypothesis (or stack thereof?) and the solution. Decide to test the opposite hypothesis; if it is proved wrong (and we are only one hypothesis away from the original board), we have *the* unique solution. Stored solutions might be usable for checking things down the road...? Not sure.
  • 3) Check the first invalid area/region on the invalidated stack to see if any rules fire.
  • 4) Whenever a rule fires:
  • a) turn the affect cell(s?) white or black. Update all affected region objects: increase cell count, and/or join regions
  • b) check (whole board? affected regions?) for violation of game constraints. If any, we have a contradiction (see above).
  • c) put the affected area on the invalidated stack. Not sure what that area should be exactly... preferably the minimal set of cells that need to be rechecked. Or maybe the minimal set of affected regions. But I don't think any regions could be easily excluded from all of the above rules.
  • 5) Once region or area has been checked and no rules fired, remove it from the invalidated stack (even remove it from every region/area on the stack that includes it?)
  • 6) Return to step 2.
  • 7) If we run out of invalidated areas, check the whole board over once more. If there are still no rules fired, we have run out of possibilities, and must declare that our solver has failed to solve the puzzle. (This does not mean it's unsolvable.)

Implementation

Objects:

• A Board, divided into width x height cells.
  • Each cell has a state: black, white, or unsolved.
  • White cells can have a number.
  • We may want more than one Board, so we can try hypothetical moves and check for contradictions, then throw away our "scribblings" without affecting the real working solution ("original board").
• Regions. Each region object stores:
• a color (I don't think we need "unsolved" regions)
• a count of known cells in the region so far
• a cell count limit (see Def 1 above); for some white regions this can be unknown at first.
• the coordinates of a cell known to be in the region (for white regions, this should be the written number if there is one in the region yet; in general this will be the first known cell in the region). We could call this a "seed" cell.
• At initialization, create a white region for each given number, containing just one cell.

Operations (methods):

• Two regions can be joined. (Yes, even white regions... because sometimes you'll start a white region without knowing which number it will connect to.)
• ... more to be done here ...

Solver implemented!

Hooray! I finally got a nurikabe puzzle solver implemented. It really wasn't that tough, but took a while. My thanks to Dr. Drake at Lewis & Clark College for his Final Project: Nurikabe. The skeleton Java code there gave me the impetus to go ahead and do it.

The solver uses about seven production rules, i.e. rules that can potentially deduce the color of certain cells without doing any trial-and-error. It applies those rules repeatedly until they no longer yield any results. Then it makes a hypothesis about a given cell being a given color. If that hypothesis leads to a contradiction, it concludes the cell must be the opposite color.

The solver is successful to a degree: it solves small-to-medium puzzles very quickly. The one at the top of the page took it about half a second. But there are puzzles it has not yet solved, such as this 24x14. However, I'm getting some optimization done, and I'm hopeful that the envelope can be pushed back a ways. I think the biggest way to improve solving time is to pick your hypotheses more intelligently: If you pick one that quickly leads to a contradiction, you've made solid progress.

Creating Puzzles

My original intent for a Nurikabe solver was not to solve puzzles per se, but to assist in creating them. The last few days, I've made my first attempts at creating my own puzzles. Here they are (via Otto Janko's Java applet):

• 6x6
• 7x7
• 8x8
• 9x9
• 10x10
• 11x11
• 11x11a
• 11x13
• 12x12
• 12x14
• 12x14a
• 24x14

Help for the Java applet can be found here. Note, the save/load state feature does not work. I'm not sure why.

I used the Nurikabe player program by Oleg Andrushko to create and test the puzzles. Each puzzle is also wife-tested for quality assurance. Kathy's getting pretty good at Nurikabe!

As you might expect, the process is trial-and-error: scatter some numbers around, and try to solve the puzzle; if you find that there can't be a solution or there's not enough information, make adjustments. You usually have to try to solve it from scratch on each iteration, lest your changes have made some of the inferences you made last time invalid. So, I'd like to have the nurikabe auto-solver help with that repetitive solving part.

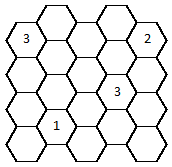
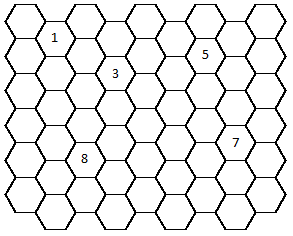
Recently I created a couple of Nurikabe puzzles on hex grids. Here they are. I don't know of an applet or any other player for such puzzles, so you'll probably have to do them on paper. Keep in mind that while a square-grid Nurikabe disallows a 2x2 block of black cells, a hex-grid Nurikabe prohibits a cluster of 3 black cells (which all share a common vertex).

Feedback

In response to my statement

What does this imply for writing an auto-solver? That if we wanted to do an exhaustive search for solutions, it would take much longer than we can afford to wait.

Adrian writes,

I'm not begging for a "who asked you?" response, but . . .

that's not really true for puzzles that are significantly small enough. For example, the three puzzles I've found on google [and the one on your web page] were solvable in a second [by the] program I wrote...

I responded,

OK, I stand corrected. I can't remember now what mental-back-of-the-envelope calculations I did, but it seemed like 2^100 was an awful lot, even with pruning.

and Adrian answered,

Well pruning is pretty serious. For a 10 by 10, you can jump down from 2^100 to 2^20 (about).

... I've looked around on the web some more (which is pretty slow because I'm stuck on dialup this week) and I've found a bunch of larger puzzles that (with my mental-back-of-the-envelope calculations) are way too big to do an exhaustive search on. Still, it works pretty fast on the small and medium sized puzzles.

(OK, I'm amending my original statement to say "for sufficiently large puzzles". --Lars)

I wrote the program in c and I really just wrote it as fast as I could type it in, so no design or OO or readability was considered.

Again, I take no credit for the readability of this program, but here it is:

http://aporter.org/nurikabe/

adrian

Jonathan wrote:

Hi Lars,

I learned of your interest in Nurikabe construction/solving after coming across your web page in a Google search. I've got a few ideas to share with you (but not a lot of time at the moment), but I did want to quickly point you to a link you might find interesting.

I think you may be reading too much into the McPhail proof of Nurikabe's NP-completeness. The fact is, NP-completeness doesn't say a whole lot about how efficiently you'll be able to autosolve in the average case, or even in the 99th percentile case. All it says is that as you scale up Nurikabe, there will exist some problems that are polynomial-intractable. These *could* be common, but they could be extraordinarily rare, too. Check out http://citeseer.ist.psu.edu/cheeseman91where.html for an excellent exposition of the relation between NP-completeness and "hardness".

I responded:

Thanks for the pointer. I'm reading the Cheeseman article with interest. I wonder if we can identify "order parameters" for Nurikabe that indicate how hard it will be to solve a particular problem?

Looking forward to hearing any ideas you have to share.

Again, please contact me if you have ideas or comments about the above, or just find it interesting.

Nurikabe Links

• Informative Wikipedia article... though editors insist on deleting lots of links they consider un-"encyclopedic".
• JDA's Nurikabe constructions
• 5x5 Nurikabe puzzles generated in real-time! And daily generated 9x9's. By Josh Metzler
• Brainteaser Programs - Puzzles - Nurikabe (in Russian) - description of rules for solving Nurikabe, and free downloadable player with sample puzzles (some of which seem to be copied from elsewhere on the Web)
• Puzzle Japan Nurikabe page - sample puzzles and tutorial, with some fairly in-depth Keys to Solving Nurikabe. (I need to check these and see if I can expand or elaborate my list.)
• Final Project: Nurikabe [broken link] for AI course at Lewis & Clark College. Includes Java class files for part of the project. The rest is up to you!